
Only the water that is above the sea level can be used to do work (e.g. The example commonly cited is the tendency for thermal differences to disappear.Examples are entropy, mutual information, conditional entropy, conditional information, and relative entropy (discrimination, Kullback-Leibler information), along with the limiting normalized versions of these quantitiesFigure 1: In a naive analogy, energy in a physical system may be compared to water in lakes, rivers and the sea. Many scientists believe that the universe is naturally evolving toward a state of maximum entropy. It has several special meanings in data communications. More generally, entropy means a process in which order deteriorates with the passage of time.
Let me explain by thinking about a deck of cards. Entropy is central to the second law of thermodynamics, which states that in an isolated system any activity increases the entropy.Answer (1 of 59): Basically, entropy measures in how many different possible ways you could configure your physical system, such that it wouldn’t change the essential features that you care about. In classical physics, the entropy of a physical system is proportional to the quantity of energy no longer available to do physical work. In an idealized state, compression is a pump, compression in a compressor and expansion in. An isentropic process is depicted as a vertical line on a T-s diagram, whereas an isothermal process is a horizontal line.


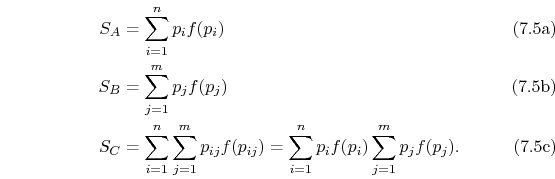
The idea was inspired by an earlier formulation by Sadi Carnot of what is now known as the second law of thermodynamics.The Austrian physicist Ludwig Boltzmann and the American scientist Willard Gibbs put entropy into the probabilistic setup of statistical mechanics (around 1875). The word reveals an analogy to energy and etymologists believe that it was designed to denote the form of energy that any energy eventually and inevitably turns into - a useless heat. 6 Connections between different meanings of entropyThe term entropy was coined in 1865 by the German physicist Rudolf Clausius from Greek en- = in + trope = a turning (point). 3.8 The main entropy theorems in ergodic theory
The absolute value of entropy is established by theNotice that when an element \(dQ\) of heat is transmitted from a warmer body at temperature \(T_1\) to a cooler one at temperature \(T_2\ ,\) then the entropy of the first body changes by \(-\frac p_\omega\log_2 (p_\omega).The formula ( 4) reduces to ( 2) if \(p_\omega = \frac 1N\) for all microstates in \(M_A\. The above formula allows one to compare the entropies of different states of a system, or to compute the entropyOf each state up to a constant (which is satisfactory in most cases). Usually, it roughly means disorder, chaos, decay of diversity or tendency toward uniform distribution of kinds.Entropy in physics Thermodynamical entropy - macroscopic approachIn thermodynamics, a physical system is a collection of objects (bodies) whose state is parametrizedBy several characteristics such as the distribution of density, pressure, temperature, velocity, chemical potential, etc.The change of entropy of a physical system when it passes from one state to another equalsWhere \(dQ\) denotes an element of heat being absorbed (or emitted then it has negative sign) by a body,\(T\) is the absolute temperature of that body at that moment, and the integration is over all elements of heatActive in the passage. Maxwell (around 1871) triggered a search for the physical meaning of information, which resulted in the finding by Rolf Landauer (1961) of the heat equivalent of the erasure of one bit of information, which brought the notions of entropy in thermodynamics and information theory together.The term entropy is now used in many other sciences (such as sociology), sometimes distant from physics or mathematics, where it no longer maintains its rigorous quantitative character. Later this led to the invention of entropy as a term in probability theory by Claude Shannon (1948), popularized in a joint book with Warren Weaver, that provided foundations for information theory.The concept of entropy in dynamical systems was introduced by Andrei Kolmogorov and made precise by Yakov Sinai in what is now known as the Kolmogorov-Sinai entropy.The formulation of Maxwell's paradox by James C. Entropy was generalized to quantum mechanics in 1932 by John von Neumann.


 0 kommentar(er)
0 kommentar(er)
